
This little book is wonderfully incomprehensible. I describe it thus because if you read it with a view to understanding it, then it rapidly gives you a dull headache, whereas if you just sit back and let it flow around you, so to speak, it has a certain charm. And if read at speed, it takes on a humour not unlike a lecture by Stanley Unwin.
Because it is so incomprehensible, it is difficult to summarise it, for the summarise something properly you have to know what the author is on about in the first place. But I will do my best.
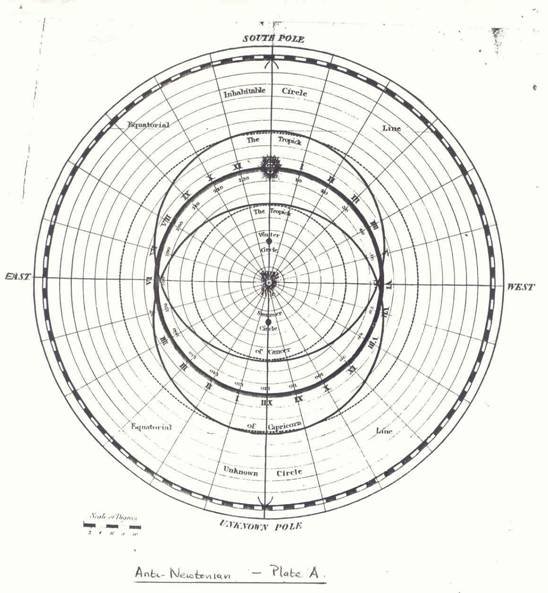
Let us begin with the author’s map of “the true system of the habitable world of land and water” (Plate A). The earth is flat, naturally, and is surrounded by an impenetrable boundary of ice. The sun moves around the equatorial circle – the one with the Roman Numerals around it – and that’s about as far as I get before I start to lose track of things. This is about half way down the first page, by the way!
“Come now”, I hear the reader say, “Surely it can’t be that bad !”
“OK,” is my reply to such readers, “Try this for size!”
“I will now take the liberty to inform any Newtonian systematic philosopher, that if he were, on the longest day standing within twenty degrees of the north pole, with his face towards the south, at twelve o’clock, he would see the sun, whose equatorial circle is only forty degrees from him; then if he were only to turn himself half round to twelve o’clock at night, he would again see the same summer’s sun, circling over some unknown place, at a distance of one hundred and forty degrees farther from him, which would be an equal distance to a south pole summer sun from the polar centre; and yet he would know that it could not be circling there; because an astronomer would affirm, at that time the south pole must be very nearly if not quite in total darkness; – in this assertion he would be perfectly correct; for then it must be circling at some reverse far distance off, over a place unknown to living man, that gulf below from whence rises the thunder’s fiery ball, which sounds the terrific warnings from an offended God; flashing its lightnings through the air, hurling its terrors and destruction on the earth beneath, from whence the reflected lights of the Aurora-boreales proceed, and streaks of cloud light stream through the open firmament, covering a darker starlight sky before it, and leaving a brighter Milky-way behind.”
Very well, let’s abandon Part I of the Anti-Newtonian as a bit on the tricky side, and move to Part II, which begins on page 16.
Folk who are foolish enough to believe that the Earth is a globe say that if you watch a ship approaching at sea, then at first only the masthead is visible, then the mast and the bow, and finally the whole thing, as the ship ‘climbs’ over the curvature of the Earth. But our author will have none of this taradiddle.

Referring to his Plate B, which I reproduce here, he writes as follows:
“First, according to my plan as represented in plate B, and shewn in Fig.2, supposing Nos. 1, 2, 3, 4, 5 and 6 to be ships in a line just appearing in sight of each other, and say twenty-five miles distance between each two ships, from No.1 to No.6, all forming a hill, or an apparent mountain of water between each two ships, and the people on board each ship will fancy ‘and which is always the case’ that they are on the hill and the other ship in the valley; then, if a third ship is placed on the centre of each convex mountain of water, caused by the first line of ships, namely, Nos. 7, 8, 9, 10, and 11, as shewn in figure 2 also, each of these centre ships will bring the one on each side to a perfect level with itself, as will appear more distinctly in figure 3, all appearing unto each centre ship alike; but on the contrary, let each ship in the first line remain as before stated, with each centre ship on its convex mountain; then, as Nos. 1, 2, &c in the first line, will form a mountain between them, so will Nos. 7, 8 &c form mountains also between them, as in Fig.1, and the first and second line of ships will be buried in the water, and so on, forming mountains of water and ships over each other, up to the clouds.”
This, I think, is supposed to be a refutation, by reductio ad absurdum, of the ‘approaching ship’ method of demonstrating the Earth’s rotundity, but it is difficult to be sure. There’s a second part to it as well, but I don’t understand that either, and so I don’t quote it here. Once again, ships are mounting up to the sky and in imminent danger of being shipwrecked in regions where “a Kendall’s Life-preserver may be of no avail.” We are now at the top of page 19, by the way, and things don’t get any clearer in the page or two following.
But there is a clear argument on page 23. It is to the effect that if the Earth, and therefore Sea, were globular, then no ship could ever be becalmed for hours, let alone days, “without gliding down this globular hill, either on one side or on the other.” Since ships do get becalmed, the ocean cannot be globular. (My favourite argument against a globular ocean was penned, if I remember correctly, by William Carpenter in the 1870s. He pointed out that if the Earth were spherical, the oceans would have long since dripped off into space.)
Another clear argument comes on page 24, where our author assures us that Newton’s idea of a ‘force of gravity’ is a nonsense incompatible with the Wisdom of God. For if God created Man to live and move in the world, is it at all likely that He would have ordained something like gravity which could only slow him down again?
Unfortunately, having had two clear arguments on two consecutive pages, our author lapses into obscurity again, and everything becomes as clear as mud. Eventually, he tires of gravity, and on page 29 launches into Part III of his book. He begins by overturning the notions of atmospheric weight and pressure, and having done that – at least to his own satisfaction, if no-one else’s – he turns to the refraction of light.
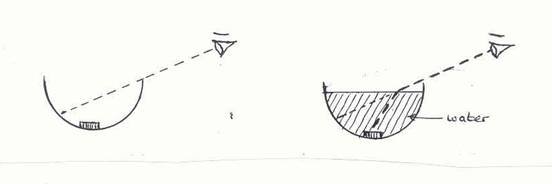
We have all of us at school seen that experiment whereby a coin is placed at the bottom of a bowl so that we cannot quite see it over the bowl’s rim. Then water is poured into the bowl, and the refraction of the light rays from the coin suddenly brings it into startling visibility, as illustrated here:
Here, now, is our author’s version of the same experiment:
“As a perpendicular ray is equally attracted on all sides; or, I say, rather refracted, but in reality equally reflected on all sides; for the bason, by its circular form, is a concave reflector; but the bason being on its bottom, and we are looking down into it, neither the bason, nor any other concave in the like situation, can reflect its own magnifying powers: but the water being a transparent body, and when poured into the bason forms a second concave upwards, and being like a spinning-top with its central point downwards, becomes a convex reflector unto the concave bason, which reflects the likeness of the shilling through the convex upwards into the concave of the water, still keeping its same apparent size; although the concavity of the bason, if it were transparent, would magnify it so as to appear five times larger than what it really is.”
Nor is that, by any means, the end of our author’s explanation. Another two or three pages of this lie in wait to confound the would-be reader, at the end of which he blithely writes:
“Although I have been obliged to abridge the various subjects, to bring them within as small a compass as possible, yet I hope I have left the whole sufficiently clear to be understood by the intelligent reader.”
Suppose we just tip-toe quietly away from this one?