Fig. 16.1
Let us now stick with earthquakes and delve a little deeper into the orthodox–unorthodox spectrum.
Almost as unlikely as Beaumont’s earthquake triggering via the magnetic pull of a passing comet or meteor was the supposedly more serious theory of John Gribbin and Steven Plagemann, put forward in their book The Jupiter Effect (1974).
Gribbin and Plagemann believed that in 1982 there would be a grand alignment of the planets. That is, all the planets of the solar system would be strung out in one long straight line radiating outwards from the Sun. At this time, they claimed, the combined effect of all the planets pulling in the same direction would trigger off earthquake activity in the Earth.
The mechanism they postulated was not so much the combined gravitational pull on the Earth as the effects it would have on the Sun. The combined tidal force, they claimed, would influence the Sun in such a way as to increase the flow of charged particles that constantly streams out from its surface. This stream of particles, known as the solar wind, is responsible for a variety of effects in our atmosphere, so that any increase in the solar wind would, in effect, stir up atmospheric turbulence. According to Gribbin and Plagemann, this increased turbulence would result in an increased atmospheric “drag” on the Earth’s rotation, the effects of which would be small but sudden changes in the Earth’s rate of spin. Any area of the Earth’s surface in which the friction between continental rafts had built up to unstable levels could then quite easily be jolted into a sudden slip (earthquake) by these jerky changes of spin. That is, the grand alignment could, via a complex chain of causes and effects, induce earthquake activity on the Earth.
California’s San Andreas Fault, which was the scene of the great San Francisco earthquake of 1906, would be particularly at risk under the grand alignment, Gribbin and Plagemann claimed. They were quite definite about this: “Within two years of 1982 (between 1980 and 1984) there will be a major disaster, probably in the Los Angeles area but perhaps in the San Francisco Bay area.”
Thankfully, the San Andreas Fault declined to act in accordance with this extraordinary theory. There is, moreover, one other minor objection. There wasn’t any real alignment at all in 1982! The planets were actually spread out over some 60 degrees of sky, and in fact there was a distinctly closer alignment in 1980, when nothing happened either. Certainly the San Andreas Fault will cause trouble eventually, but Jupiter will almost certainly have had nothing to do with it.
Reverting now to our observations on the orthodox–unorthodox spectrum, the idea of a grand alignment triggering an earthquake is almost astrological in character, as even Gribbin and Plagemann admit in the preface to The Jupiter Effect.
Likewise embarrassingly close to the spirit of astrology was a short paper printed in the journal Nature for 18th July 1959, in which Dr R. Tomaschek published an account of his curious observations regarding earthquakes and the position in the sky of the planet Uranus at the time of their occurrence.
In a study of serious earthquakes recorded in the present century, Dr Tomaschek found that Uranus was close to its upper or lower transit of the meridian of the epicentre in an unexpectedly high proportion of cases. The correlation was particularly marked, Dr Tomaschek claimed, for earthquakes occurring in 1904 to 1906 inclusive. In 1906, he noted, Uranus entered into direct opposition with Neptune, though he did not claim this fact as significant in any way. In fact, Dr Tomaschek didn’t claim to know why Uranus seemed to have an earthquake association at all, and concluded with the remark that it might not be “a relationship of cause and effect in the usual mechanical sense.”
Before going on we should perhaps consider the gravitational pulls which the planets exert on the Earth, as this is obviously the first thing one thinks of in connection with theories like the Jupiter effect or Dr Tomaschek’s observations about the apparent effects of Uranus. Just what effects do the planets have on the Earth, gravitationally speaking?
Much the most important and massive planet is Jupiter. In fact, Jupiter’s mass is greater than those of all the other planets combined; Saturn comes next, but has only 95 times the mass of the Earth, as against 318 earth-masses for Jupiter. The values for the other outer planets are much less; 17 earth-masses for Neptune, only 14 for Uranus. As for Pluto, it seems to be a puny thing – perhaps a large ice-ball. It is quite definitely far less massive than our Moon, and the idea of its having any effect upon the San Andreas Fault (or any other fault) is frankly weird.
Even if all the planets lined up, their combined pulls would be almost inappreciably greater than those of Jupiter and Saturn combined. And remember, too, that the main pull on Earth comes from the Sun – if it didn’t, our orbit would be very different from the one we actually follow. (The Sun’s pull on the Earth is far, far stronger than that of the Moon. True, the lunar tides are stronger than the solar ones, but that is only because of the greater difference in pull exerted by the Moon on the moonward and far sides of the Earth’s globe.)
Which brings us to the knotty problem of earthquake prediction in general. Geologists have been puzzling over this one for years, but so far they freely admit that they haven’t got very far. In fact, so desperate have they been to find any method of prediction – orthodox or otherwise – that in the late seventies the United States Geological Survey took to keeping files of predictions sent in by amateurs. These included predictions based on astrology, dreams, psychic forebodings and just plain old hunches. In fact anything that anyone cared to send in.
Over the period of collection they logged upwards of 2500 predictions sent in by more than 230 amateur earthquake-prophets, but when the predictions were matched against occurrences, the scores were little better than pure guesswork.
Of course, there are always claims of successful predictions after the event, and a few vague ones, sometimes, from before the event. An example of each can be cited in connection with the great English earthquake of 1884 (for which see Peter Haining, The Great English Earthquake, published in 1976.)
Geologically speaking, England is a very stable little island, so that earthquakes are few and far between. They are not unknown, though, and the most destructive ever known here occurred on 22nd April 1884. It was centred on the rural farming areas to the south-east of Colchester, and though over in less than a minute, the shock was felt up to 150 miles away.
On the day of the great English earthquake, a correspondent signing himself “W.W.S.” wrote a letter to the East Anglian Daily Times. He began by quoting I Corinthians 14.22 (what else?) and went on (in part):
The Ancients say, When you find at the vernal equinox the close proximity of Saturn to the cusp of the fourth house of the heavens in Gemini it pre-signifies earthquakes and high winds in the Western parts, viz., England, London and the United States &c. This was the position on Thursday, 20th March 1884. The serious earthquake shock in Essex and Suffolk this day is, to say the least, a strange coincidence.
Of this letter the Editor of the East Anglian Daily Times wrote: “What a pity W.W.S. did not write last week.” We suspect that the Editor shared our own views of prophecies which emerge from the woodwork after the events they are supposed to prophesy.
On the other hand, in the first week of April, 1884, the astrological column of the London Daily Echo predicted that during that month there would be “an upheaval in eastern England of a kind not before experienced.”
The question is, of course, whether one counts such a prediction as unequivocally referring to the earthquake, or whether in fact the prediction was neatly twisted to fit the events after they had happened. It is rather like reading in your horoscope one morning that you are “due for a windfall”, and coming home that same evening to find your chimney stack blown down. Is that a fulfilled prediction or isn’t it?
But to return to the problems of earthquake prediction, it is entirely understandable that geologists would like a method of prediction that is totally free of the vagaries and double meanings associated with many types of prophecy. Which is where Alfred Jopling Cooper comes in, because, when it came to predicting earthquakes, Mr Cooper had no doubt at all that he had got it all taped, and with scientific precision to boot.
We are back again at that ill-defined boundary between orthodox and unorthodox, because Mr Cooper’s ideas are something of a riotous extension of Dr Tomaschek’s.
Mr Cooper began his studies in the late nineteenth century. Having been shipwrecked three times by stormy weather, on three consecutive voyages, he decided to set about finding a method of predicting where and when stormy weather would strike. He wrote:
On the west coast of South America I was frequently disappointed by the non-arrival of a calculated storm, until it became apparent that on these occasions an earthquake took the place of an absent storm.
This showed that under some conditions the same forces which brought about a tempest, under other conditions caused an earthquake.
Twenty-three years of study of these forces resulted, in 1910, in the publication of his extraordinary book on the subject: Solectrics: A Theory Explaining The Causes Of Tempests, Seismic and Volcanic Disturbances, And How To Calculate Their Time and Place.
The term “solectric” seems to have come from the compound “solar electricity”, for Mr Cooper believed that the solar system was governed by an all pervasive, multi-purpose, partly electromagnetic power called Solectric Power. He put it like this:
The term solectric power may be defined as the power which the sun exerts on every member of the solar system. … Solectric power is the combined energy emanating from the sun, which, when analysed or resolved into its component forces, includes light, heat, chemical action, gravity, electricity, and vital force, according to circumstances and surrounding conditions.
In some ways, solectric power acts like static electricity insofar as the planets get solectrically charged up by the Sun. As they move in their orbits with respect to the Sun and each other, their “charges” attract and repel each other to varying degrees, and, on occasion, solectric discharges occur between them. On such occasions a solectric “spark” will pass either directly from a planet to the Sun, or else from one planet to another and thence back to the Sun. (According to Mr Cooper, the Sun generates all the solectric power in the solar system, radiating it out to the planets, and charging them up. But then one way or another that power must eventually return to the Sun.)
All the Earth’s climatic effects, from heatwaves to hurricanes, as well as earthquakes and volcanic eruptions, are the results of discharges of pent-up solectric energy from the Earth.
The Earth is like an electrically charged sphere inside an insulating layer (the atmosphere). Discharges follow lines of least resistance and for this reason are particularly prone to happen in mountainous districts where the Earth reaches up into the atmosphere like a lightning conductor. Less severe discharges may happen over the relatively flat expanses of the ocean, and these give rise to such phenomena as waterspouts – the ocean’s version of a lightning conductor. Similar solectric discharge effects occur on other planets, incidentally.
Now, such discharges can occur only when the planets have the right configurations with respect to each other. Consequently, hurricanes, tornadoes, quakes and volcanic eruptions can only happen when conditions are astronomically ripe for them.
In order to set down Mr Cooper’s theory in terms understandable to the general reader, we must first define a couple of technical terms. Firstly, we shall say that the ‘angle’ between two places on the Earth’s surface is the angle subtended by those two places at the centre of the Earth. Secondly, we shall define the ‘Sun point’ at any given moment to be that point on the Earth’s surface at which the sun is directly overhead. The Moon point, the Venus point and so forth are similarly defined.
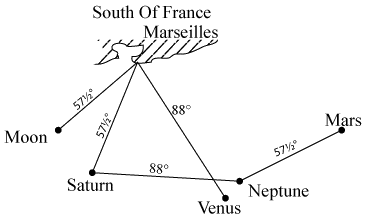
Now, a place on the Earth’s surface becomes solectrically active whenever the Sun point or the Moon point makes an angle of 57½° or 88° with the place in question. The situation is solectrically aggravated when combinations of planetary points reinforce the action of the Sun or Moon. An example will make this clear.

Fig. 16.1
On 11th June 1909 at 9.06 p.m. GMT, an earthquake shook the south of France. Fig. 16.1 shows the solectric situation of Marseilles at the time of the quake. As can be seen, the Moon point makes an angle of 57½° with Marseilles. Venus and Saturn reinforce the Moon, with their points forming angles of 88° and 57½° respectively with Marseilles. Meanwhile, Neptune and Mars have an indirect effect insofar as the Neptune point makes an angle of 88° with that of Saturn, and the Mars point 57½° with that of Neptune. Thus, Mars acts solectrically on Neptune; Neptune acts on Saturn; and Saturn acts directly on Marseilles itself.
According to Mr Cooper, the Sun is the central generator of the solectric power cycle, and as such is the primary solectric influence in the solar system. Thereafter, the solectric pecking order, at least as regards effects on the Earth, runs as follows: 1. The Moon; 2. Jupiter; 3. Venus; 4. Mars and Saturn; 5. Uranus and Neptune; 6. Mercury.
Mr Cooper’s book catalogues dozens of hurricanes, gales, waterspouts, storms, heatwaves, earthquakes and volcanic eruptions, each case accompanied by a solectric diagram like Fig. 16.1. All of these events are shown to be consequences of planetary interaction at angles of 57½° and 88°. Figs. 16.2, 16.3 and 16.4 give solectric interpretations of a violent snowstorm, a waterspout and a volcanic eruption respectively.
Fig. 16.2
Fig. 16.3
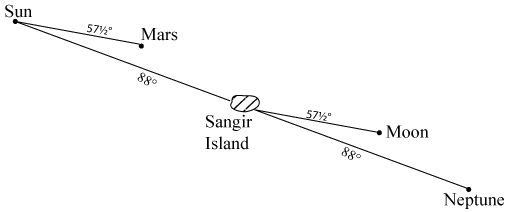
Fig. 16.4
Incidentally, Mr Cooper never did explain the significance of the 57½ and the 88 – he merely found them to work and left it at that. He did hazard a guess that these two angles represented “different conditions of solectric force, such as positive and negative”, but the precise mechanics of solectric interaction remained shrouded in a good deal of mystery. For example, he never really did sort out why some solectric configurations led to heatwaves or cyclones, whereas other very similar configurations led to volcanic eruptions. Nevertheless, his catalogue of case histories provided a common solectric background for these diverse phenomena, and this in itself was quite something. At least to Mr Cooper.
Actually, we’ve simplified Mr Cooper’s theory a bit, because not all atmospheric or seismic phenomena have a solectric explanation quite as straightforward as those summarised in Figs. 16.1 to 16.4. Mr Cooper found that sometimes it wasn’t the Sun point that governed an event but one of the Sun’s “supplementary points”. There are two of these, one having the same longitude as the Sun point but opposite latitude and the other having the same latitude but opposite longitude. For example, if the Sun point is at 100° W and 15° N, then its supplementary points are at 100° W, 15° S and 80° E and 15° N, and either of these points can as easily govern a solectric phenomenon as the Sun point itself.
Then there is the “nadir Sun”. This is opposite the Sun point in both latitude and longitude. For example, if the Sun point is at 100° W and 15° N, then the nadir Sun point is at 80° E, 15° S. This point, too, can solectrically govern events as effectively as the sun point itself.
The Moon and each of the planets likewise each have two supplementary points and a nadir point, so that the reader can be forgiven for thinking that with all these points, supplementary points, and nadir points, dotted about the globe (36 in all!), one would be hard pressed to find a corner of the world not in imminent danger of solectric discharge of one sort or another. The more so when one considers that errors of up to 2 or 3 degrees or even more either way are allowed in a 57½° or 88° angle.
However, we consider this argument to be an unwarranted slur on a marvellous theory that plunges ever deeper into solectric meridians, differences in solectric hour angles, the effects of eclipses on earthquakes, and the dangers of the Moon approaching its limiting declinations.
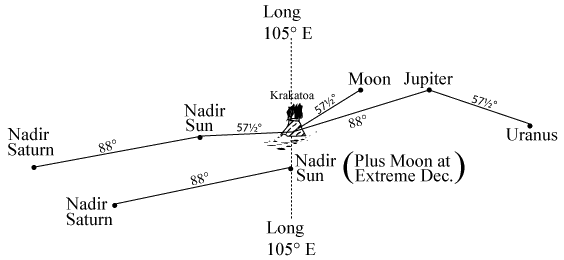
Fig. 16.5
In Fig. 16.5, for example, we give a solectric portrait of Krakatoa. The upper lines show the position on 26th August 1883, 8.53 p.m. GMT, the volcano being under the direct influence of the Moon, Jupiter and the nadir Sun. The nadir Sun point is boosted by the nadir Saturn point, whilst the Jupiter point is enhanced by Uranus. Earlier that same day, at 5 p.m. GMT (lower diagram) the nadir Sun was on the solectric meridian of Krakatoa, with the nadir Saturn in attendance at an angle of 88°. At this time, too, the Moon was at its extreme northerly declination (i.e. point furthest north of the equator), and this is always a signal of strong solectric activity:
An immense wall of cloud was observed with bursts of forked lightning, like large serpents, rushing through the air. Balls of fire rested on ships’ mastheads and extremities of yardarms.
The rest is violent volcanic history.
Meteorites, too, are of solectric origin. Mr Cooper wrote:
If a tremendous volume of solectric force is hurled against an irresponsive earth, the surrounding gases in its path between, say, Jupiter and the earth are caught and fused together, and these are changed into metals. The solectric forces tend to become latent in solidity and we see on a small scale the making of a world.
Hence the points of impact of meteorites are governed by the now familiar patterns of 57½° and 88° solectric angles.
Mr Cooper’s ideas on comets were similarly solectric. He believed that every comet orbited two suns, one our own and the other a distant star, “thus lightly linking up two far distant solectric systems.”
In fact Mr Cooper saw solectric powers in action wherever he looked, from the creation of life and the power that keeps the Earth spinning on its axis, to the destructive forces of an earthquake or volcano. He wrote:
The Solar System is so rigidly and beautifully linked up that not a shock in Saturn nor a tremor in Venus takes place without a sympathetic thrill through the earth and a response from the rest of the planets.
And on the scale of human rather than cosmic affairs:
It is not too much to assert that, judging from actual cases, the planets strike down or kill, while if the sun is assisted by the moon, madness takes place, and riots in such places as asylums.
It is worth remembering that Mr Cooper was a very caring man. He wanted to find a means of predicting, and thus avoiding, the large-scale human tragedies frequently associated with natural disasters. It is worth remembering, too, that he did all his calculations before the advent of electronic calculators and mini-computers, and that in itself was no mean feat. His book is a remarkable instance of Independent Thought.
The most celebrated exponent of modern earthquake control was Mr P. Norcott, of Broadstairs, who in 1970 published a little booklet entitled Bigger and Better Earthquakes. Unlike most astronomers, he believed that the Earth was formed by material splashed out of the Sun when it was hit by a huge meteor. Be that as it may, according to Mr Norcott the Earth’s rotation is slowing down, and therefore the centrifugal force around the equator is decreasing; pressure is building up below the crust, and eventually something has to give way, resulting in an earthquake.
If we could stop the slowing-down of the Earth’s rotation, then, clearly, earthquakes would cease. One of Mr Norcott’s answers (he has three) is to use gyroscopic force. Build huge flywheels, erect them at the North and South Poles, and start them whirling. They will, so to speak, give the Earth ‘a bit of a spin’, and thus keep the rate of rotation constant!
There is, however, a second method. The Moon influences the slowing-down of the Earth’s rotation via the tides; by building vast dams to stop the ocean waters from sloshing around from one sea-basin to another, tidal friction can be more or less eliminated.
The third alternative, of course, is to slice the Moon in half, towing one hemisphere of it round to the far side of the Earth so that the contrary gravitational forces will cancel each other out. Just how this could be achieved is, admittedly, a problem, but no doubt it could be solved with sufficient application.
Clearly close attention must be paid to this matter. If nothing is done, earthquakes will continue; if anyone has a better answer than Mr Norcott’s, we would be delighted to hear about it.
We now come to the Coons Theory of Wet and Dry Steam.
Burton C. Coons was a retired inventor and machine designer who lived in Honolulu. After forty years of pondering the forces involved in the generation of earthquakes, volcanoes and tidal waves, he came to the conclusion that such violent phenomena simply could not result from the stresses and strains generated in geological faults. In his opinion, only steam could generate sufficiently large forces to cause these things.
According to Mr Coons, sea water seeps down into pockets of molten lava beneath the Earth’s crust. The water immediately turns into steam – wet steam, that is – and this rapidly becomes dry steam as the moisture is removed from it. This dry steam then expands “as fast as lightning, in all directions, looking for a way out”, and in doing so it causes first earthquakes and second either volcanoes or tidal waves, depending on whether the steam blows out through the land or through the sea.
We had better explain a little about wet and dry steam, more particularly the latter, which to the uninitiated may sound like a contradiction in terms. Wet steam is always visible, Mr Coons assures us, whereas dry steam is not. This is because dry steam has had its moisture dried out, and so it is essentially an air-like gas. “Wet steam confined has a 200-pound pressure per square inch,” Mr Coons tells us. “When changed into dry steam it immediately has a 650-pound pressure per square inch.” Dry steam is dangerous stuff, then.
Incidentally, Mr Coons once worked for the New York Central Railroad when he was a young man, and it was his job as a fireman on soft-coal-burning locomotives which gave him his knowledge of the awesome power of dry steam. For example, he once saw a heavy steel boiler explode when the water in it was very low and the coals had been left burning beneath it. Obviously, he deduced, the water had evaporated, the wet steam had turned to dry steam, and boom! The eruptions of Mauna Loa and Mount Etna are similar explosions on a larger scale, and as evidence that his theory is correct Mr Coons points out that one of the first things to appear at the start of a volcanic eruption is steam.…