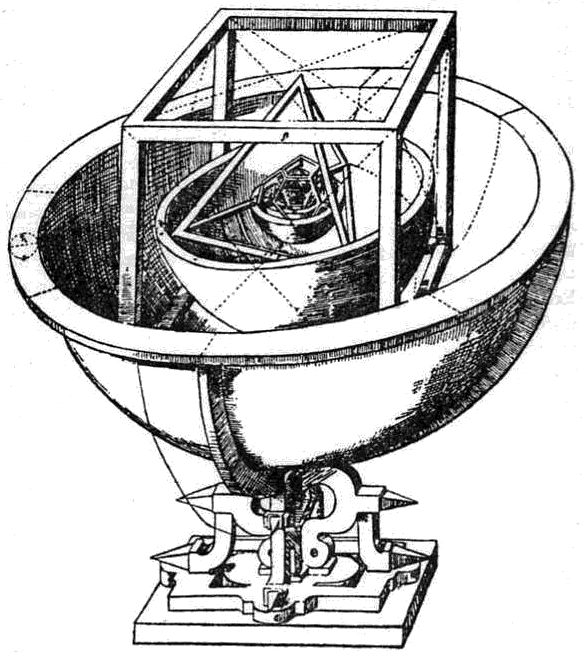
Fig. 8.1
The story of science – particularly astronomy – is peppered with colourful characters. Of special note was Tycho Brahe, an eccentric Dane who had a false nose (his own had been sliced off in a student duel!) and whose observatory included a prison cell as well as a pet dwarf who was reputed to have second sight. Tycho was an expert observer who drew up the best star-catalogue of his time, but until his death, in October 1601, he declined to believe that the Earth might be in orbit round the Sun. He preferred a curiously hybrid system, according to which the Sun moved round the Earth, but the planets circled the Sun.
Tycho’s last assistant was Johannes Kepler, who will always be remembered as being the man who proved that the Sun is indeed the centre of the planetary system – but that the orbits of the planets are ellipses, not circles. Kepler had his own problems, too: he had to supplement his income by casting horoscopes, and he also faced a crisis when his mother was brought to trial as a witch. (She was eventually acquitted, though by all accounts she looked every bit ‘witchy’.)
In many ways Kepler was modern in his outlook, but in others he was firmly rooted in the past. He believed that each planet must have a sphere or layer of space in which it is dominant; so that no space should be wasted, these spaces should touch each other, and he decided that the answer was to be found in the five regular solids of geometry: from the cube (six equal faces) to the icosahedron (twenty). He fitted these solids in with the spaces between the planets, using the following sequence: Saturn – Cube – Jupiter – Tetrahedron – Mars – Dodecahedron – Earth – Icosahedron – Venus – Octahedron – Mercury (see Fig. 8.1.)

Fig. 8.1
That is, the five regular solids separated the six then known planets, each solid being inscribed and circumscribed by the planetary spheres either side of it. The model worked to quite a tolerable accuracy and Kepler always regarded it as the greatest of all his discoveries. It was published in 1596, in a book with the snappy little title of Prodromus Dissertationem Cosmographicarum continens Mysterium Cosmographicum de admirabili Proportione Orbium Coelestium deque Causis Coelorum numeri magnitudinis motuumque periodicorum genuinis et propriis, demonstratum per quinque regularia corpora Geometrica. Tycho Brahe, at least, was impressed, and did not look disapprovingly down his false nose! Unfortunately, of course, Uranus, Neptune and Pluto later turned up to spoil the mathematical harmony of what had been a really elegant theory, but by then Kepler was long dead.
Another of Kepler’s ideas was that the planets had to be constantly ‘pushed’ along by some effect of the Sun, as otherwise they would stop in their tracks. As an addendum, he claimed that universe began with the planets stretched out in a line from the Sun, out to the origin of the Zodiac, and that the universe would end when the same thing happened again – though unlike most end-of-the-worlders, he stopped short of giving a definite date.
Actually, this last idea is one which dates back to classical times. For example, the Roman author Seneca, in his Natural Questions, refers to a current theory which ascribed catastrophes to the movements of the planets. The Earth would be destroyed by fire when all the planets lined up in the sign of Cancer, and would be destroyed by water when all the planets lined up in the sign of Capricorn, these being the signs of the summer (heat) and winter (cold) solstices. We shall see a modern re-emergence of such ideas in chapter 16.
Even when the layout of the solar System had been firmly established, efforts were made to find a hidden meaning behind the overall picture. For instance, there is the curious relationship known as Bode’s Law, though it was actually discovered by a mathematician named Titius. It runs thus: to find the mean distances of the planets from the Sun, start with the following simple sequence of numbers: 0, 3, 6, 12, 24, 48, 96, 192, 384. From 3 onwards, each number is double the preceding one. Now add 4 to each number, giving the sequence: 4, 7, 10, 16, 28, 52, 100, 196, 388. Now divide by 10, giving the sequence: 0.4, 0.7, 1.0, 1.6, 2.8, 5.2, 10.0, 19.6, 38.8. This sequence models, quite remarkably, the actual sequence of the mean distances of the planets from the Sun, as follows:
| Body | Actual | Bode’s Law |
|---|---|---|
| Mercury | 0.39 | 0.4 |
| Venus | 0.72 | 0.7 |
| Earth | 1.00 | 1.0 |
| Mars | 1.52 | 1.6 |
| 2.8 | ||
| Jupiter | 5.20 | 5.2 |
| Saturn | 9.54 | 10.0 |
| Uranus | 19.19 | 19.6 |
What is remarkable is that when Titius (1766) and Bode (1778) first spotted this ‘law’, Uranus hadn’t been discovered, and yet it fitted the ‘law’ when it was discovered in 1781! Furthermore, the ‘law’ seemed to ‘predict’ a missing planet between Mars and Jupiter, which was precisely where the asteroids later turned up – Ceres, the first, was discovered in 1801. Though the ‘law’ gained some respect after these ‘successes’, it lost it again when Neptune was discovered in 1846, and was found not to follow the pattern – its mean distance from the Sun was 30.06 compared with a Bode’s Law prediction of 38.8. When Pluto turned up in 1930, Bode’s Law fared even worse, and the ‘law’ was effectively abandoned as a numerical curiosity.
Admittedly Bode’s Law was a purely scientific concept and did not involve any form of mysticism. But the idea of searching for “God’s Plan” in the planetary system did not die out with Kepler, and even in the twentieth century it was far from fading away. This brings us to 1940, and the publication of Frank Lonc’s booklet The Key to the Cosmos.
Mr Lonc believed that the key to the layout of the solar system – the key to the entire cosmos, even! – lay in one number, phi. Phi is equal to 1.618 and a bit. It is a number which has fascinated mathematically minded people with occult inclinations for hundreds of years.
Since we do not intend in this book to delve into mathematical crankery, fascinating as it is, we must content ourselves with saying that phi is a number encountered repeatedly in the geometry of the mystical five-pointed star, or pentagram, and that sages and seers persist in seeing it at the root of anything and everything from human anatomical proportions and the harmony of nature to the Great Pyramid and the design of the Solar System.
Frank Lonc was the undisputed champion of phi. Every corner of creation from the tiniest atom to the entire galaxy seemed to be governed by it. Mr Lonc saw phi operating where others saw nothing at all, and because he saw it as universal, he named it “The Cosmic Constant”.
Orthodox scholars did not share his enthusiasm. They claimed that phi was nothing but a harmless mathematical toy and that Mr Lonc was forcing it into a universe that would have worked quite happily without it. At best, he was making a mountain out of a molehill; at worst, he was crackers.
But this did not worry the steadfast Mr Lonc, who believed that the scientists had all been hoodwinked by the charade of Einstein’s Theory of Relativity. In Mr Lonc’s opinion, Relativity was a load of incomprehensible gobbledegook which had been accepted by scientists because they couldn’t understand it, and they didn’t want to lose face by admitting it. Don’t let it worry you if you can’t make head or tail of Relativity, was Mr Lonc’s philosophy, because there isn’t an ounce of sense in it anywhere. Would God, in all his wisdom, have created a universe that ran according to such hopelessly complicated mathematical formulas? No, answered Mr Lonc emphatically. He’d have opted for a much simpler arrangement built upon one single Cosmic Constant like phi. Thus it came about that Mr Lonc decoded the blueprint for the Solar System.
Starting with the Earth 1 unit from the sun, multiply by phi to give 1.618 units, the distance of Mars from the Sun. Multiply this by 1.618 again to give the distance of the asteroid belt from the Sun, and so on. Each planetary orbit has a radius phi times that of its predecessor.
Working the other way, and starting again with the Earth say 1 unit from the Sun, divide by phi to give the distance of Venus from the Sun, then divide by phi again to give the distance of Mercury from the Sun.
The scheme is summarised in the table below, and aside from the fact that some of the planets seem to have wandered away from where God put them and Mr Lonc wanted them, plus the small matter of a missing planet between Jupiter and Saturn, it all works rather splendidly.
Unfortunately, the world of orthodox astronomy didn’t share this view, and like band of learned donkeys, plodding along after a relativistic carrot on a string, they continued to worship Einstein’s theory at the expense of Mr Lonc’s.
| Planet | Distance from Sun, Earth = 1 | |
|---|---|---|
| Lonc | True | |
| Mercury | 0.382 | 0.387 |
| Venus | 0.618 | 0.723 |
| Earth | 1 | 1 |
| Mars | 1.618 | 1.524 |
| Asteroids | 2.618 | 2.65 |
| Jupiter | 4.236 | 5.203 |
| Missing? | 6.854 | ??? |
| Saturn | 11.090 | 9.539 |
| Uranus | 17.944 | 19.182 |
| Neptune | 29.034 | 30.058 |
| Pluto | 46.979 | 39.52 |
Another extraordinary excursion into the problems of the hidden harmony of the Solar System was the subject of a paper delivered before the Literary and Philosophical Society of Liverpool by Mr James Smith on 25th January 1864. It bore the grandiose title, On the Relations existing between the Dimensions and Distances of the Sun, Moon and Earth.
The harmony was hidden, Mr Smith claimed, because astronomers were in such a muddle over the actual measurements of the dimensions and distances involved. Almost at the drop of a hat, he claimed, astronomers would “adjust” their estimates of the distance of the Sun by a colossal 4 million miles, and when it came to guessing the distance of Neptune, they couldn’t be at all sure to within 100 million miles. Little wonder that they couldn’t see the subtlety of the relationships involved – it was lost behind a mountain of errors.
The astronomers’ muddle started with the size of the Earth itself. In Mr Smith’s day, to measure the distance to the Moon you couldn’t just do it by sitting in an arm-chair and bouncing laser beams off the lunar surface. Laser beams just hadn’t been invented. The only way to measure distance in the 1860s was by trigonometrical surveying, and that implied an accurate knowledge of the size and shape of the Earth. But, as Mr Smith pointed out, some astronomers weren’t all that sure of the diameter of the Earth. He wrote:
Now, it will be obvious to you, sir, and to every member of this society, that if we are unable to ascertain truly and exactly the dimensions of our own planet, the Earth, we must forever remain ignorant of the true dimensions of the other celestial bodies composing our solar system, for this is the source from which all our information on this subject is derived, and the base upon which all our knowledge rests. And it is equally certain that a very slight error in the Earth’s diameter and distance from the Moon leads to errors of enormous magnitude in the dimensions and distance of the Sun and of all the still more distant bodies – the planets.
Casting aside the unreliable figures of orthodox astronomy, Mr Smith drummed up his own more harmonious figures – or, as he himself saw it, glimpsed the truth behind the approximations and the guesses bandied about by the astronomers of the day. The following table gives the orthodox figures (as of 1864) and Mr Smith’s figures for various diameters and distances, in miles:
| Quantity | Orthodox Value (as of 1864) | Mr Smith’s Value |
|---|---|---|
| Earth’s Diameter | 7912 | 8000 |
| Moon’s Diameter | 2160 | 2000 |
| Sun’s Diameter | 880,000 | 960,000 |
| Earth–Moon Distance | 237,000 | 240,000 |
| Earth–Sun Distance | 95,365,000 | 115,200,000 |
Adopting Mr Smith’s figures, the harmony of the Solar System becomes immediately apparent. Thus:
Earth–Moon distance = 120 × Moon’s Diameter
Sun’s Diameter = 120 × Earth’s Diameter
Earth–Sun Distance = 120 × Sun’s Diameter
Mr Smith claimed that these relations gave “a demonstration of the littleness of man’s wisdom, and the superlative wisdom of the great Creator.”
The rest of the Liverpool Literary and Philosophical Society weren’t so sure. According to a report of the meeting:
The Chairman said that notwithstanding the elaborate calculations of Mr Smith, which were very ingenious, they were not one bit nearer the matter than they were before. He assumed that if the heavenly bodies did exist at these supposed distances at which he made them out there would be a great harmony and beauty in the solar system, but whether harmony did exist or not was a question that had to be proved by observation.
This was really a polite way of asking which was more reliable – the measurements of orthodox astronomers or the assumptions of Mr Smith. Being well aware of the opposition which his paper would evoke, Mr Smith wrote:
The mathematical and astronomical authorities who have attempted to write me down a fool, may, and probably will, continue to make a mystery of their craft, and jealously guard it, but I venture to tell them that they may fiddle upon the strings of their mathematical ingenuity until their heads ache but they will never succeed in controverting these mathematical and geometrical truths.
A few years before Mr Smith, Mr John Wilson (whom we met in the last chapter, of course) had done battle with the weighty matters of the harmony of the Solar System in his book The Lost Solar System of the Ancients Discovered (1856). As Mr Wilson saw it:
Thus the square of the number of ½ diameters of the moon that equal the diameter of the earth will equal as many ½ diameters of the earth as equal the ½ diameter of the moon’s orbit.
Or the cube of the number of ½ diameters of the moon that equal the diameter of the earth will equal as many ½ diameters of the moon as equal the ½ diameter of the orbit of the moon.
And again:
Thus the square of the number of ½ diameters of the earth that equal the diameter of the sun will equal as many ¼ diameters of the earth as equal the semi diameter of the earth’s orbit.
Also the number of semi diameters of the earth that equal the diameter of the sun will equal as many semi diameters of the sun as equal the semi diameter of the earth’s orbit.
We assume that all this is as clear to our readers as it is to us.
Even orthodox astronomers are not averse to spotting patterns in the dimensions of the Solar System. G.F. Chambers in his Handbook of Descriptive and Practical Astronomy (1889) wrote:
The following coincidences may or may not deserve to be mentioned:
Finally, in a footnote, Mr Chambers wrote:
Many attempts have been made by ingenious dabblers in Astronomy to discover other arithmetical coincidences formed after the spirit of Bode’s Law. The following is the only one I have met with which deserves reproduction. Take the series 0, 1, 2, 4, 8, 16, 32 and 64: add 4 to each and the resulting figures represent with some approach to accuracy the relative distances of the satellites of Saturn from their primary.